La Función Escalón: Una Herramienta Esencial en Redes Neuronales
Las redes neuronales artificiales son modelos computacionales diseñados para imitar el comportamiento del cerebro humano. Estas redes están conformadas por elementos llamados neuronas, que reciben y procesan información a través de conexiones llamadas sinapsis. En este contexto, la función escalón es una herramienta esencial en el funcionamiento de las redes neuronales.
En este artículo, discutiremos qué es la función escalón, por qué es esencial en redes neuronales, las ventajas y desventajas de su uso y algunos ejemplos de aplicación en la vida real.
¿Qué es la función escalón?
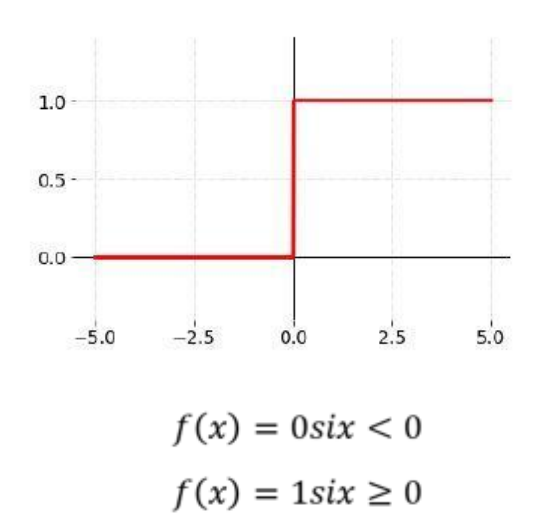
La función escalón es una función matemática simple que toma un valor de entrada y devuelve una salida binaria. Es decir, si la entrada es mayor o igual a un cierto umbral, la salida es 1, y si la entrada es menor que el umbral, la salida es 0. Formalmente, la función escalón se define como:
$$f(x) = begin{cases} 1 & text{si } x geq 0 0 & text{si } x < 0 end{cases}$$
La función escalón se utiliza comúnmente en redes neuronales para modelar la activación de las neuronas en respuesta a la entrada de información.
¿Por qué es esencial en redes neuronales?
Las redes neuronales artificiales se basan en el procesamiento de información a través de conexiones entre neuronas. La función escalón es esencial en este proceso porque permite que cada neurona decida si debe activarse o no en función de la entrada que recibe.
En una red neuronal, la entrada de una neurona está multiplicada por un peso y sumada a la entrada de otras neuronas conectadas a ella. Si la suma de entrada supera un umbral, la neurona se activa y envía su salida a las neuronas conectadas a ella. De lo contrario, la neurona permanece inactiva y no envía ninguna salida.
La función escalón permite que la neurona modele esta decisión de activación / inactivación en forma binaria. Por lo tanto, es esencial en la implementación de los modelos de red neuronal.
Ventajas y desventajas de la función escalón
Una de las ventajas de la función escalón es su simplicidad. Es fácil de implementar y computacionalmente eficiente. Además, la función escalón es una herramienta poderosa para modelar problemas binarios o de clasificación, donde solo se espera una salida binaria.
Sin embargo, la función escalón también tiene algunas desventajas. En particular, la función escalón no es diferenciable, lo que significa que no se puede usar con algoritmos de aprendizaje automático que requieren cálculos de gradiente. Además, la función escalón no es adecuada para modelar problemas en los que se esperan salidas continuas o en los que se espera que la salida sea una función suave de la entrada.
Ejemplos de aplicación en la vida real
La función escalón se utiliza en una variedad de aplicaciones en la vida real. Por ejemplo, en la detección de spam, la función escalón se puede utilizar para clasificar correos electrónicos como spam o no spam. En la detección de objetos en imágenes, la función escalón se puede utilizar para determinar si un objeto está presente en una imagen.
En el campo de la visión por computadora, la función escalón se utiliza comúnmente en los cálculos de mapas de características. Un mapa de características es una representación de una imagen que identifica las características relevantes de la imagen para su posterior procesamiento. La función escalón se puede utilizar para calcular los valores de las características en función de la entrada de la imagen.
En resumen, la función escalón es una herramienta esencial en las redes neuronales artificiales. Es fácil de implementar y computacionalmente eficiente, pero tiene algunas limitaciones en términos de su capacidad para modelar problemas continuos y su falta de diferenciabilidad.
A medida que las redes neuronales artificiales se vuelven cada vez más sofisticadas y complejas, es posible que la función escalón se reemplace por funciones más avanzadas y flexibles. Sin embargo, la función escalón seguirá siendo una herramienta importante en la comprensión y el diseño de redes neuronales.