Las redes neuronales son una herramienta poderosa en el mundo de la inteligencia artificial y el aprendizaje automático. Uno de los elementos clave de las redes neuronales es la función sigmoide, una función matemática que ayuda a las redes a procesar y categorizar datos de manera efectiva. En este artículo, exploraremos la función sigmoide, cómo se implementa en las redes neuronales, sus ventajas y desventajas, y algunos casos de uso prácticos.
La función sigmoide: Introducción y definición
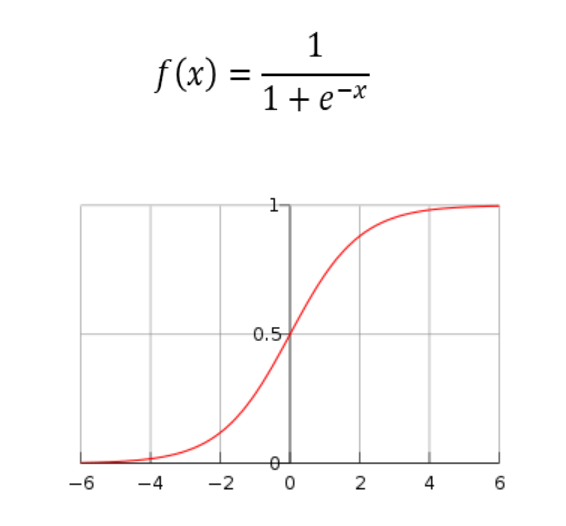
La función sigmoide se utiliza comúnmente en las redes neuronales como una función de activación para las capas ocultas. Esta función toma un valor de entrada y lo comprime en un rango comprendido entre 0 y 1, lo que la convierte en una función útil para modelar probabilidades y realizar clasificaciones binarias. La función sigmoide tiene una forma característica de «S» que le da su nombre.
La fórmula de la función sigmoide es la siguiente:
$$f(x) = frac{1}{1+e^{-x}}$$
Donde $e$ es la constante matemática e y $x$ es el valor de entrada. Cuando $x$ es grande y positivo, la función se aproxima a 1, mientras que cuando $x$ es grande y negativo, se aproxima a 0. En el punto medio, la función tiene un valor de 0.5.
Implementación de la función sigmoide en redes neuronales
En las redes neuronales, la función sigmoide se utiliza como una función de activación para las capas ocultas. La entrada a la función es la suma ponderada de las entradas de una neurona y sus pesos sinápticos. La salida de la función se utiliza como entrada para la siguiente capa o como salida final de la red.
La función sigmoide también se utiliza en el proceso de entrenamiento de las redes neuronales. Durante el entrenamiento, se ajustan los pesos sinápticos para minimizar la función de pérdida. La función sigmoide se utiliza para calcular la derivada de la función de pérdida en función de los pesos, lo que permite que el algoritmo de aprendizaje actualice los pesos de manera eficiente.
Ventajas y desventajas de la función sigmoide
Una de las principales ventajas de la función sigmoide es su suavidad y la facilidad de derivación. La función es diferenciable en todos los puntos, lo que permite que los algoritmos de optimización trabajen con ella de manera eficiente. Además, la función sigmoide es monótona creciente, lo que significa que una entrada mayor siempre producirá una salida mayor, lo que la hace útil para modelar relaciones de causa y efecto.
Sin embargo, la función sigmoide también tiene algunas desventajas. Uno de los problemas es que la función se satura cuando los valores de entrada son grandes, lo que significa que la derivada de la función se acerca a cero y el aprendizaje se ralentiza. Además, la función sigmoide no es simétrica, lo que significa que las entradas negativas y positivas se procesan de manera diferente, lo que puede afectar el rendimiento de la red.
Casos de uso y ejemplos prácticos de la función sigmoide en redes neuronales
La función sigmoide se utiliza en una amplia gama de aplicaciones de redes neuronales. Se utiliza comúnmente en redes neuronales para la clasificación binaria, como en la detección de spam o la clasificación de imágenes. También se utiliza en la modelización de probabilidades, como en la predicción de la probabilidad de lluvia o en la detección de fraudes financieros.
Un ejemplo práctico de la función sigmoide en acción es en la detección de enfermedades cardíacas. Los médicos pueden utilizar las redes neuronales para analizar datos de pacientes y predecir si un paciente tiene un mayor riesgo de enfermedad cardíaca. La función sigmoide se puede utilizar para modelar la probabilidad de que un paciente tenga una enfermedad cardíaca, lo que puede guiar las decisiones de tratamiento y prevención.
En resumen, la función sigmoide es una herramienta clave en las redes neuronales. Se utiliza para modelar probabilidades y realizar clasificaciones binarias, y se implementa como una función de activación para las capas ocultas. Aunque tiene algunas limitaciones, la función sigmoide es una herramienta valiosa para procesar y categorizar datos de manera efectiva.
Como hemos visto, la función sigmoide es una herramienta esencial en el mundo de las redes neuronales. Al comprender cómo funciona y cómo se implementa en las redes, podemos utilizarla de manera efectiva para resolver una amplia gama de problemas de aprendizaje automático. Con su capacidad para modelar probabilidades y realizar clasificaciones binarias, la función sigmoide seguirá siendo una herramienta clave en el futuro de la inteligencia artificial y el aprendizaje automático.