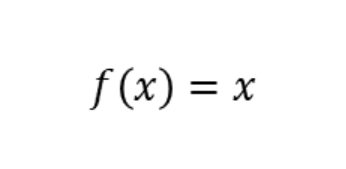Las funciones de activación son fundamentales en el aprendizaje y entrenamiento de redes neuronales artificiales. Una de las funciones más simples y comunes es la función lineal. En este artículo se abordará la definición, características, implementación y limitaciones de esta función en el contexto de las redes neuronales.
Función Lineal: Definición y Características
La función lineal es una función matemática muy simple que se define como f(x) = ax + b, donde a y b son constantes. Su nombre se debe a que su gráfica es una línea recta. Esta función es muy útil en la representación de relaciones lineales entre dos variables.
Entre las características más importantes de la función lineal se encuentran su dominio y rango infinitos, su pendiente constante y su intercepto en el eje y. Además, es una función continua y derivable en todos sus puntos.
Función Lineal en Redes Neuronales Artificiales
En el contexto de las redes neuronales artificiales, la función lineal se utiliza principalmente en la capa de salida para la regresión lineal. En este caso, se busca predecir un valor numérico continuo a partir de un conjunto de entradas.
La función lineal también puede utilizarse en la capa de entrada para normalizar los datos de entrada, es decir, transformarlos de un rango determinado a un rango entre 0 y 1.
Función Lineal como Función de Activación
La función lineal también puede utilizarse como función de activación en las capas ocultas de una red neuronal. Sin embargo, su uso se limita a casos muy específicos, ya que su principal limitación es su incapacidad para modelar relaciones no lineales.
En la práctica, se utilizan otras funciones de activación no lineales, como la función sigmoidal y la función ReLU, que permiten modelar relaciones no lineales de forma más efectiva.
Ventajas y Limitaciones de la Función Lineal
Una de las principales ventajas de la función lineal es su simplicidad y eficiencia computacional. Además, su uso en la capa de salida para la regresión lineal es muy útil en problemas donde se busca predecir un valor numérico continuo.
Sin embargo, su principal limitación es su incapacidad para modelar relaciones no lineales. En la mayoría de los casos, es necesario utilizar funciones de activación no lineales para lograr una mayor precisión en el modelo.
Otra limitación de la función lineal es su sensibilidad a los valores atípicos (outliers), ya que estos pueden afectar significativamente la pendiente de la recta y, por lo tanto, la precisión del modelo.
En conclusión, la función lineal es una función de activación común en las redes neuronales, especialmente en la capa de salida para la regresión lineal. Si bien es una función simple y eficiente, su uso se limita a casos específicos debido a su incapacidad para modelar relaciones no lineales. En general, es necesario utilizar otras funciones de activación no lineales para lograr una mayor precisión en los modelos de redes neuronales.