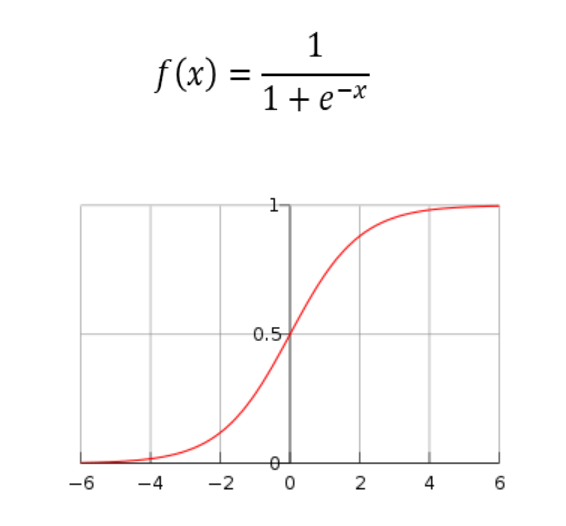
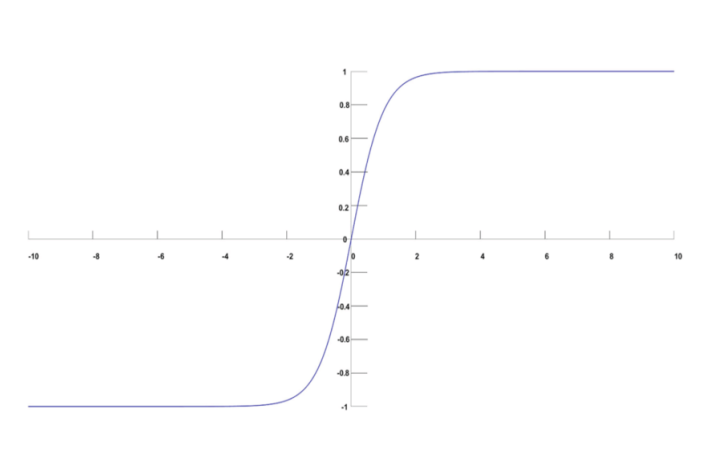
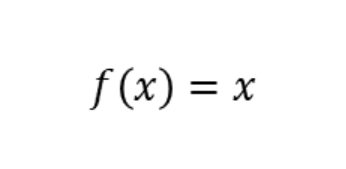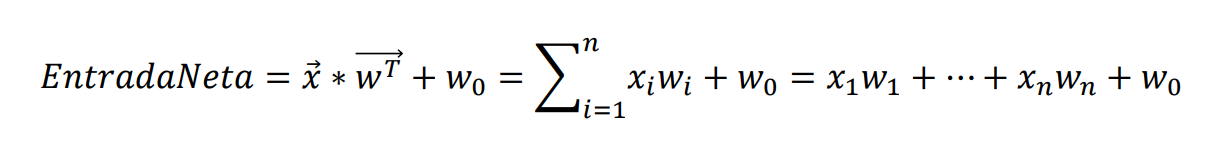La función sigmoide es una herramienta clave en redes neuronales debido a su capacidad para modelar la relación no lineal entre entradas y salidas. Al ser una función continua y diferenciable, es útil para la optimización de parámetros mediante técnicas de aprendizaje automático. Además, su forma de curva en S permite que la salida de la red se encuentre en un rango limitado, lo que mejora la estabilidad y la precisión del modelo. En resumen, la función sigmoide es fundamental para el éxito de las redes neuronales.
Leer másFunción SoftMax: Activación para la clasificación
La Función SoftMax es una herramienta esencial en la clasificación de datos en Machine Learning. Su uso es fundamental para obtener una distribución de probabilidades que permita determinar con precisión la clase a la que pertenece un objeto. En este artículo, exploraremos en detalle las propiedades y aplicaciones de esta función de activación.
Leer másLa Función Leaky RELU y su papel en las Redes Neuronales
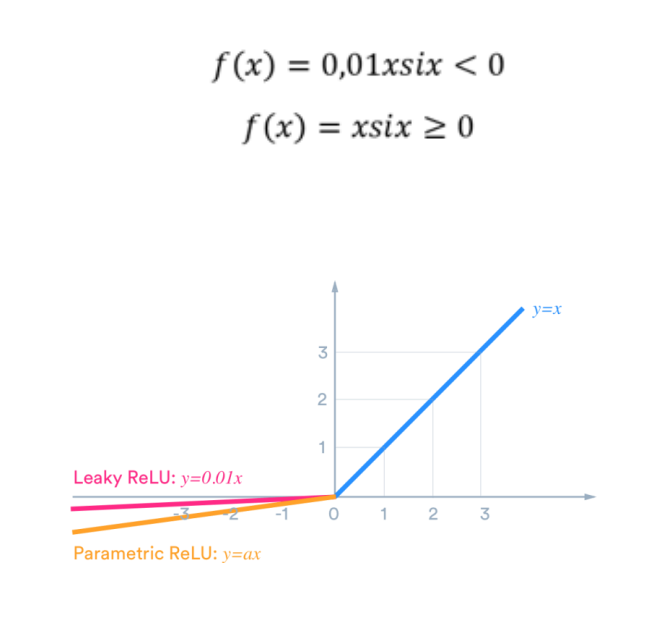
La Función Leaky RELU es una variante de la función de activación RELU que soluciona el problema del «neurona muerta». Su papel en las redes neuronales es mejorar la precisión de los modelos y reducir el riesgo de sobreajuste.
Leer másLa Función Unidad Rectificada Uniforme (RELU): Una Herramienta Esencial para el Aprendizaje Profundo
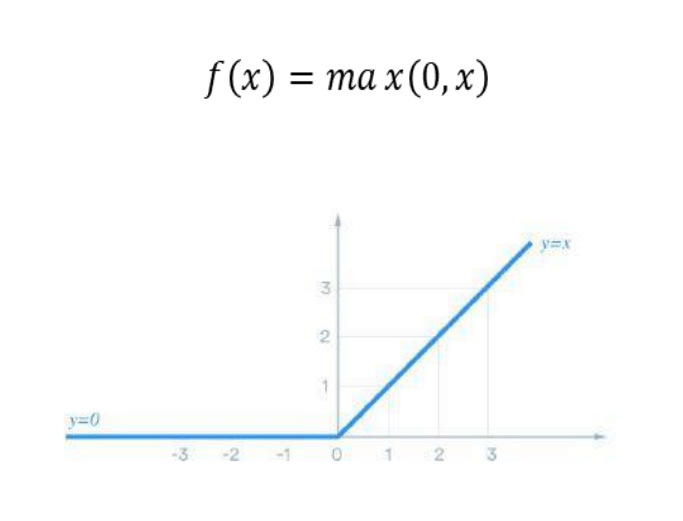
La función unidad rectificada uniforme (RELU) es una herramienta esencial para el aprendizaje profundo debido a su capacidad para mejorar la precisión y velocidad de los algoritmos de aprendizaje automático.
Leer másLa Función Escalón: Una Herramienta Esencial en Redes Neuronales
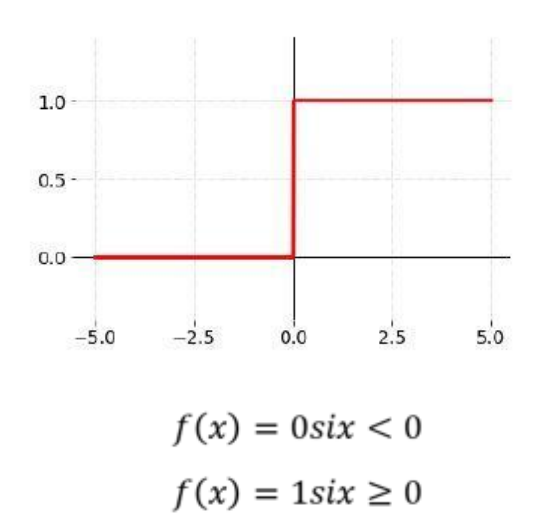
La Función Escalón es una herramienta esencial en redes neuronales ya que permite la activación de las neuronas y la clasificación de los datos de entrada. En este artículo analizaremos su funcionamiento y su aplicación en diferentes modelos de redes neuronales.
Leer másFunción Lineal: Una Función de Activación Común.
La función lineal es una de las funciones de activación más comunes utilizadas en el aprendizaje automático y la inteligencia artificial. Esta función es simple y efectiva para modelos que requieren una salida lineal o proporcional a la entrada. La función lineal se representa como f(x) = mx + b, donde m es la pendiente y b es el punto de intersección con el eje y. Aunque esta función es limitada en términos de complejidad, es una herramienta valiosa para muchos problemas de modelado.
Leer másLa Red Neuronal Totalmente Conectada: Un Enfoque Innovador en el Aprendizaje Automático
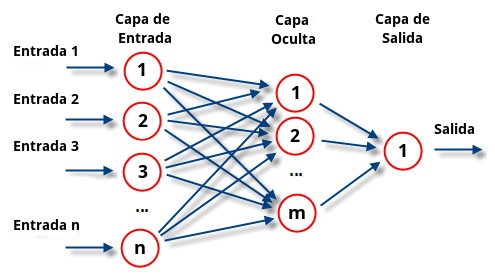
La red neuronal totalmente conectada es una técnica innovadora en el aprendizaje automático que permite un mayor grado de precisión en la predicción de datos. Con un enfoque basado en la retroalimentación continua y el ajuste de pesos, esta red es capaz de aprender y adaptarse a nuevos datos de manera eficiente y efectiva. En este artículo, exploraremos los fundamentos de esta técnica y discutiremos su aplicación en diversas áreas de la industria y la investigación.
Leer másFormulación Matemática de Entrada de Red Neuronal Artificial
La formulación matemática de la entrada de una red neuronal artificial es esencial para comprender el proceso de aprendizaje de la red. Esta entrada se compone de vectores de características que se utilizan para entrenar la red y hacer predicciones precisas. En este artículo, analizaremos la teoría detrás de la formulación matemática de la entrada y cómo se aplica en el aprendizaje supervisado y no supervisado de las redes neuronales.
Leer másRedes neuronales multicapa: avanzando en la inteligencia artificial
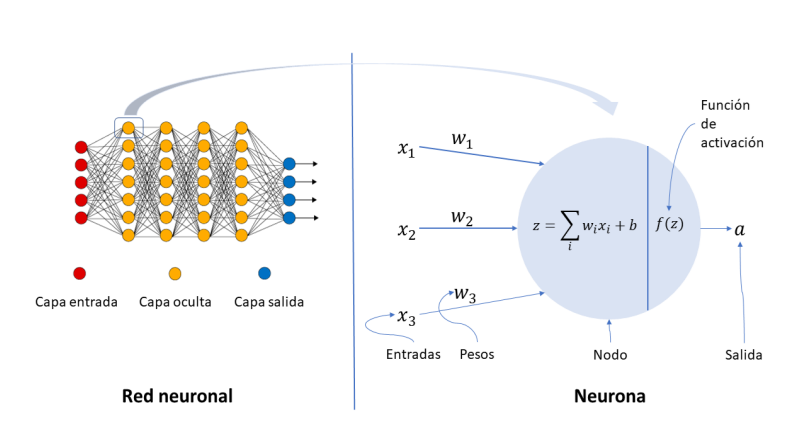
Las redes neuronales multicapa han permitido un gran avance en la inteligencia artificial al simular el funcionamiento del cerebro humano y permitir un mejor procesamiento de información compleja.
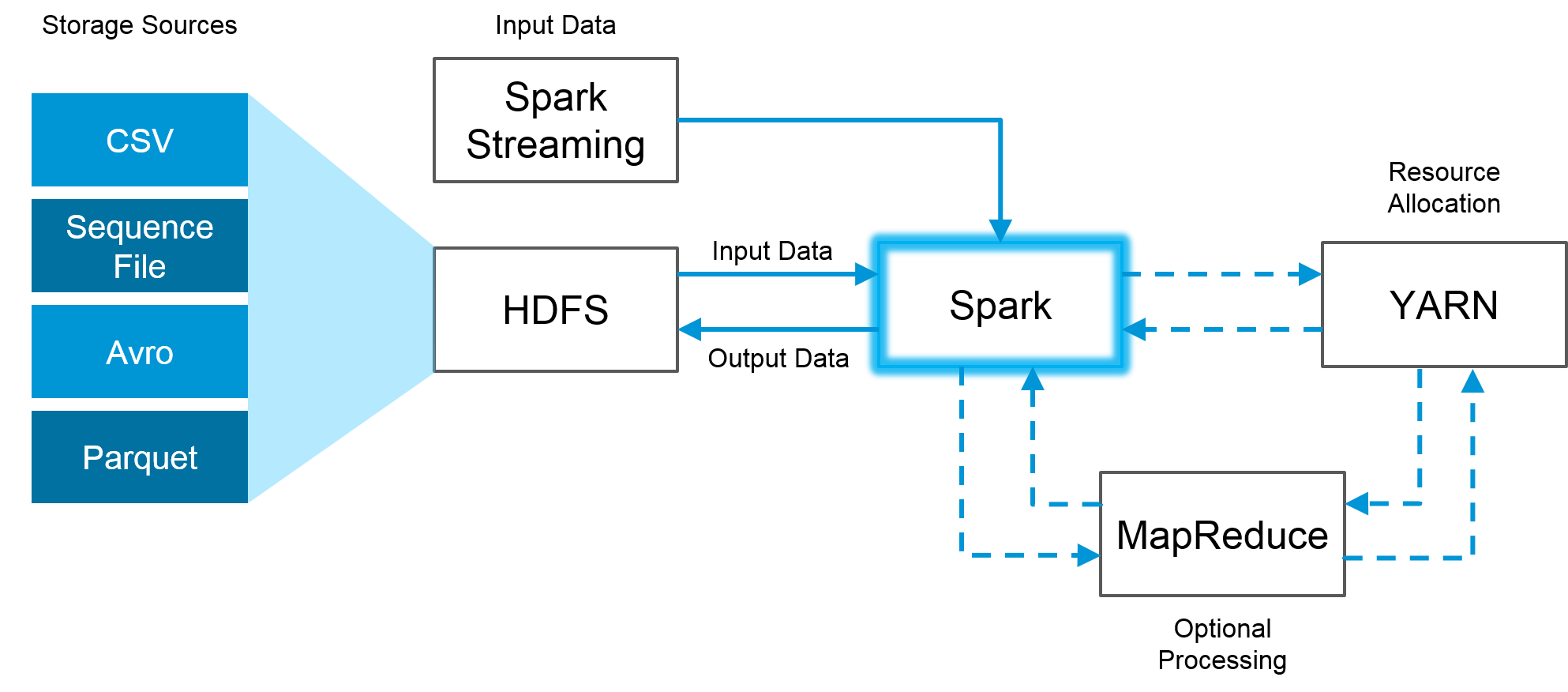
Leer másDataframes y Pipelines en Spark: Optimización de Procesamiento de Datos
Spark permite optimizar el procesamiento de datos a través de la utilización de dataframes y pipelines.
Leer más